Loci on the Argand Plane
Introducing Loci on the Argand Plane GGB
On TES.com you can find this:
What they need to remember
There are three basic types of complex locus which my students need to know about:
Type 1: | z - a | = r
Type 2: | z - a | = | z - b |
Type 3: Arg(z-a) = alpha
This tool is to play around with Argand diagrams to encourage the students to understand the geometry in each equation. I want them to know:
z - a is like a vector AZ
| z - a | is the distance AZ
we want to draw every possible z which satisfies the equation - that is what a locus is
Arg(z - a) is the angle between the real-axis direction and the vector AZ, in radians.
Lesson Outline
In my lesson starter, I include a question about plotting two complex numbers on an Argand diagram: w, z and z - w. Show how z - w is equal to the vector WZ.
Then I introduce loci, the three types that they need to be able to recognise and use. I'll mention how there are generally two ways to understand them, "Algebraic" which is easier to understand but takes a bit longer and "Geometric" which is more sophisticated, but harded to explain.
For each type, show them the algebraic method for solving these problems:
Replace z with x +iy,
tidy up reals and imaginaries
use Pythag for the modulus
tadaa - its an equation you recognise.
This way works but is rather time-consuming and it only works properly for Types 1 & 2. So I want them to appreciate the geometry too...
Sort-of Scripted Guided Discovery
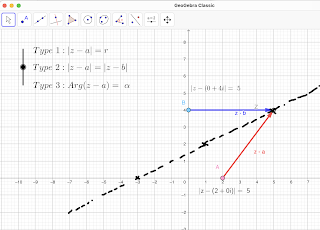
Let’s say you want to use an example like: | z- 2i | = 5
You might use a script like this - try to rephrase if necessary to elicit the responses from the students. The image is projected over the whiteboard and I get students up to draw all over the board.
Which type of locus is it: Type 1.
What is a? 2i
What what does that look like if you plot it? (0,2) (drag the point A to (0,2)
This is an Argand Diagram, so what should the axis labels be? (Billie writes "Re" and "Im")
Dave, has Billie written them the right way round?
What is does "z - a" look like? (Remember from the starter?) The vector AZ / A line joining A to Z
What do these two little lines (|z - a|) mean? Modulus of z-a
What is the modulus of z-a - what does it mean on the screen? Length of the red vector
What is the length / magnitude of the vector currently? (Reads it off)
Does my Z satisfy the equation | z - 2i | = 5? No (Mark the point and draw sad face next to it.)
Where does Z need to be for the equation to be satisfied?
(Tom and Dick don't know. Ask Harry to plot the point.)
Thanks Harry. Is Harry right, Tom? Dick? (Ask a few others if they agree - vote on it.)
How do you know Harry is right / wrong?
(Move the Z point to that position - indicate where the distance is shown - and if it is right, draw a happy face.)
Well done Harry! Are we finished now? Oh, you think so…
Do you think we’re finished Phil? No? Why not? There is another point that satisfies the equation
I guess you’re right Phil, there might be another solution - where is the other solution? Can you plot it for me?
(Smiley face)
So we're finished now, right? Are we? vote
Why do you think we're not finished Jessie? (Surprised) Are there more solutions? Can you draw some more solutions for me? How many solutions are then Jessica?
(Check the distances by dragging the Z point over each of Jessie's points. Smiley faces abound.)
We've got quite a lot of points on the screen now. What do we notice about them? Can we find every single solution? Why not?
How can we represent an infinite number of solutions on the graph?
What shape it it? What is the minimum information you need to describe that shape exactly?
Right, I have another example for you: | z - 2 - 3i | = 7. What will this look like?
Just look at it for a minute and then check with your partners, what they think. See if you agree with each other.
What shape do you think it will be Derek?
(Get them to draw it, then check it is correct by dragging points around on the screen. )
Do you get the idea? Lots of back and forth and checking questions to make sure they are keeping up.
Then depending on how they are getting on more examples or repeat the process with the other types.
Once they have tried a few, you can push them a bit further.
More challenge
"What if I change the equals sign into a less-than-or-equal-to?"
(You can use the tool to show inside the circle, the distance is less than or equal to the radius (smiley face) and outside the circle the distance is larger (sad face)
"What if there are two inequalities: | z - 2 | < 5 and 0 < Arg(z) < pi/2?"
Special Maths And: An intersection of two shaded regions.
"What will this one look like: | z | = 2 | z - 3 | ?"
It is easy to interpret geometrically but that doesn't help to draw it: z is twice as far away from the origin as it is from the point (3,0). If you use the algebraic method it falls out easily - surprisingly it is a circle.
"What about this one? ¼ + Im(z) = | z – ¼ i | "
The distance from Z to the line y = - ¼ ("directrix") is equal to the distance from Z to the point (0, ¼ ) ("focus") - it is a parabola. You can use the algebra method: (Im(z) = y)
So ¼ + y = | x + i(y - ¼ ) |
Worth mentioning
Kids hate using radians for some reason, so I've used degrees on my GGB page, but the equations have to be in radians. This was a conscious decision - I want them to understand the meaning of Arg(z) easily and I want them to remember how to convert units.
If you can't draw on the screen because it is a TV screen or something, there is a pen option on Geogebra in the top left corner:
Thanks for reading.
If this is useful for you, please write a review on TES.com.
Comment below with your ideas for using it differently and making it better.

Comments
Post a Comment