Further Mechanics: Collisions part 1

Collisions appear on the syllabus for Mechanics M1 and Further Mechanics. 

On M1,  the students only learned about direct (one-dimensional) collisions and only needed to use Conservation of Momentum to solve the problems. 

In Further Mechanics we need to teach Newton's Experimental Law (with the Coefficient or Restitution) and solve problems with direct and indirect particle-barrier collisions and particle-particle collisions.

I've made some Geogebra pages to teach this topic:

1) Particle-Barrier Collisions

Find this resource on TES

Here's my outline plan for next time I teach it. I'm planning to use it to introduce the coefficient of restitution.

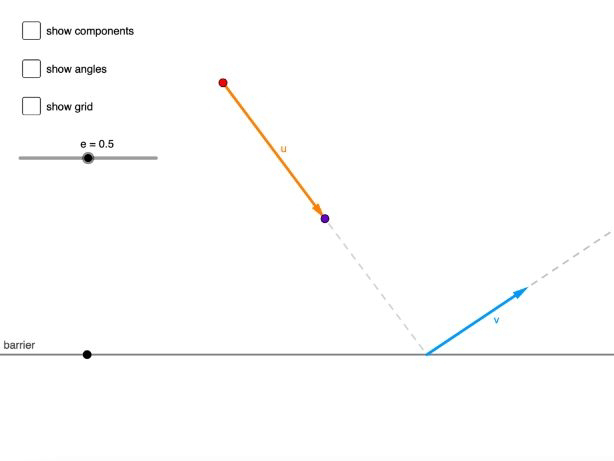
Typically, I start this topic by comparing particle-barrier collision with light reflecting on a mirror and try to elicit that angle of incidence = angle of reflection does not work unless e=1.

I'll use the Geogebra page which uses Newton's model and get them to draw a table of angles for a few different values of e. 

Dont say anything much about e, but start with e=0.2, then measure a handful of different angle-in / angle-out pairs. Then repeat the process with a different table for e=0.6 and e=1.0.

If I can get hold of one of those old wooden board protractors, and the projector doesn't stretch the image and distort the angles, I'll do this as a class using the tool and volunteering students to help me with the angles.

Or they can measure it on their iPads  - perhaps delete the "show angle" checkbox on the version you share with the class. Maybe a printed worksheet with the angles drawn. (I'll make one and include this on TES.)

If you are teaching remotely, why not get each student to fill in separate cells in a shared collaborative spreadsheet. (Maybe you can do this on Google? I'm in China so I would use DingTalk) Assign different measurements to different students. There's nowhere for lazy students to hide, and you should get lots of data points. Then plot nice curved graphs easily using the spreadsheet. You should get nice straight lines when you plot tan vs tan.

The angle-in & angle-out will (in general) be different, but it's maybe not so obvious that the ratio of the tan of the angles is the same as e. Can you lead them to this result without telling them? If not then show them and ask them to check it. Write it down - we'll come back to it.

Next question will be: why is this? 

We want the students to recognise that the parallel-component of the velocity is not affected by the collision, and the ratio of the perp-components is equal to the e-value. Hopefully we can elicit this from the class using the "show components" option. 

To facilitate this you might want to show the values of the components. (I'll add an option for this.)

Remember:

Parallel to barrier, nothing changes 

Perpendicular to barrier, can you get the students guess Newton's experimental law? 

Get it written down, in students' own words. At least two versions.

" v_perp = e x u_perp" 

"Speed out = e x speed in"

Do you need a negative sign? (no for speed / yes for velocity). Its ok to get technical about projected vectors along a perpendicular line. You can mention the Line of Action.

What does e tell you about a collision?

"e is a measure of how bouncy a collision is"

Explore some different situations and say whether e is large, small,  0, 1? If you have them use a bouncy ball / ping-pong ball, a squash ball, a tennis ball, a book.

Job done.

Then do example problems, direct, indirect, forwards, backwards then practice questions from textbook.

Extension questions:

- If the final speed is 50% of the initial speed and e=0.75, what were the angles? (Not checked - does this work?)

- by considering parallel and perpendicular components of u and v, explain why tan(beta) against tan(alpha) gives a straight line.

- double collisions with barriers at right-angles , and then angles which are not so friendly. Same e, different e. 

Suggested optional homework: 

- use tan(beta)/tan(alpha)=e to measure the coefficient of restitution for different kinds of balls bouncing off walls, using video and measuring angles. How closely does the experiment match the model at different approach angles? Make a <3 minute video on Flipgrid describing the experiment and the findings.

For other teaching ideas and modifications, I welcome your suggestions.

In Part 2, I will write about teaching particle-particle collisions. I have two more Geogebra tools for this. One for detail and one for fun.