Powers of Complex Numbers

You can download it here.

Hi guys,

I dug out an old Geogebra project and dusted it off. It is about complex numbers, calculating powers and thinking about what happens on the Argand plane when complex numbers are mulitplied together.

Here are my ideas about how to use this tool:

1) Practice multiplication and understanding multiplication on the Argand plane in terms of the modulus and argument:

• Inquiry Qn in the corner of the board: “What do complex products look like on an Argand diagram?”

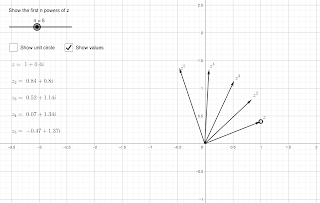
• Starter (on the board):  “z = 1 + i, calculate z^2, z^3, …”  Give a fixed amount of time and challenge the class to calculate as many as they can in the time. If necessary, demo the process with z^2 and z^3. Perhaps suggest using a recursive process, eg: z^3 = z x z^2. Some might want to try using binomial expansion instead (Extn Qn “Which method is better? Why?”).

• After the time has elapsed, hand out some pre-drawn Argand axes and give them two minutes to sketch all their answers. Set up the tool with n = 1,  and drag the circle on the tip of z to the point representing 1 + i. Use checkboxes to hide moduli and show values. Invite volunteers to draw their solutions on the axes. Do they look right? Is there a pattern? Drag the n slider up to make the solutions appear on the board. Perhaps ask pairs or groups to calculate the modulus of each solution and then check the answers using the checkbox. Invite students to explain what is happening in this sequence. 

• You can then repeat the process with a different z, say z = 2 - i. Adjust the axes by zooming out a bit (Notice (2 - i)^5 = -39 - 41i )  If they have studied binomial expansion, then perhaps you can save some time by giving different n-values to different groups and get them to write and draw their answers on the board after they are calculated. It's then easy to check the correct answers.

• Questionning and class discussion:

• What do you notice about the shapes of the graphs? Make a prediction about powers of another z - check it using the tool.

• What do you notice about the “lengths” of the “arrows”? What is the connection between the “getting bigger-ness” and z? What is a better way to ask these questions, using appropriate terminology? 

• What do you notice about the angles between adjacent “vectors”? Why should it be equal for all? What is the significance of the angles between z^x and z^{x+1}? 

• What would happen if z is multiplied by a different complex number? (Try a few examples w: calculate wz and sketch both w and wz together.) 

• Can they interpret this in terms of the modulus and argument of z?

• Complete the sentences (think pair share - good examples on board and copied into notes.): 

• “The modulus of the product of two complex numbers is…” (the product of the two moduli)

• “The argument of the product of two complex numbers is…” (the sum of the two arguments)

• “On an Argand diagram, when I mulliply by z, this is the same as… ” (enlarging the arrow by |z| and rotating by arg(z) (radians) in the anti clockwise direction)

2) Exploring Roots of unity

[Assuming that the tool was used before, as in (1)]

- Inquiry qn written in the corner of the board: “z^n=1 has how many solutions?”

- Make sure the unit circle is not shown at the beginning. Start by reminding the class what the graph shows, and show the spiral shape when n=10 and |z| is slightly larger than 1, for example z = 1-0.5i.

- Think-pair-share to interpret what is happening on the graph. Change the z value, for example z=0.8+0.5i. Invite students to interpret the graph again. 

    - Why is one spiraling outwards and one spiraling inwards? 

    - What would be the turning point, when it stops spiraling out and starts spiraling out?

- Reveal the unit circle using the checkbox. With n=1, take an example of a z with modulus=1, for example z=0.8+0.6i, ak them to predict where z-squared and z-cubed will go, etc

- Ask the class "How can we use this to explore the inquiry question?" Elicit, or nudge the class towards solving z^n=1 with different values of n, when n=1, n=2, n=3,...  write them at the side of the board and ask how can we solve each in turn.

    n = 1 - only one solution, hopefully trivial     z =1

    n = 2 - is z=1 still a solution? Are there any more solutions? Recall quadratic equations - solve by factorising a difference of two squares...

    n = 3 - Is z=1 still a solution? Is z=-1 still a solution? How many solutions do we expect to find? How can we use our Geogebra tool to find a solution? Where should z be placed so that z^3 sits on 1+0i? That's one solution, but we are expecting 3 solutions. Predictions? Test using tool. 

That's all I have so far. Maybe I will come back to this later with more ideas. 

Any suggestions in the meantime?